In the previous post I described the motivation for and some background of our ventilator project. In this post I’ll dive a little deeper with some juicy details.

To reiterate and expand somewhat on the previous post: Because this project started in response to a lack of available ventilators for the COVID-19 pandemic response, it needs to be easily manufactured, at scale, and with a minimum of special equipment. When Apple, Tesla, and Dyson make their ventilator designs, they have factories of specialized equipment available and supply chains to tap into. This project isn’t for them, though they are welcome to use it (but contact us if you want to work together).
Instead this is designed so that a small group of dedicated individuals could make a few dozen of these machines with little-to-no specialized skills, typical garage equipment, readily-available parts that can be ordered – some of which they can find at a local store, and on a modest budget.
Equally as important, the control mechanism of this project can be used independently, used with other mechanical designs and software systems. This is encouraged, as different designs will serve different purposes and be made of parts that are available in different circumstances.
You can look here for the exact parts list, directions for assembly, and some instructions on how to use it for testing.
This has not been approved for use on any living thing by any authority, and is just an incomplete proof of concept at this stage. Please, be safe.
What We’re Missing
This project is currently incomplete, but we’re publishing what we have with the hopes for collaboration. Here’s a brief list of some of the things we’re missing:
- Means of measuring volume – open to suggestions for a readily and cheaply available method for measuring volume of air-flow along with pressure
- Front-end remote UI – the system is designed to be easily attached to a REST or GraphQL API, or broadcast and controlled over MQTT, but those components and the UIs that would consume them are yet to be designed, as we focused on the actual motion so far
- Physical UI – there should be physical buttons and a display by the patient for control of the device as well
State Machine and Error Detection
Overall, the system is fairly simple (except for the motion control system that we’re using underneath of it all): We have a target pressure, we feed it into a PID control loop (explained later), use the result as a target velocity that we then jerk-limit (explained even further down), and the motion system constantly adjusts the position to achieve the requested pressure.
In operation, the target pressure needs to change with careful timing to create the inhale/exhale pattern. There are exceptions and edge cases that can occur that may be ignored or be a critical error, depending on when they occur.
Luckily, this is exactly the sort of problem that state machines were designed for, and this is the one we came up with:
There are four states:
- Idle – waiting
- Start – this could also be called “inhale”
- Hold – the target pressure has been achieved, hold there
- Release – this could also be called “exhale”
Also, there are a few events that will trigger a transition change:
- Parameters Changed → Start
- BPM (Breath-per-minute) timer expired → Start
- Pressure Achieved → Hold
- Hold Timer Expired → Release
- Position Reset (limit switch hit) → Idle
- Position Over-extended (bag is smashed completely) → Release
- Position Under-extended (motor didn’t move off of switch) → Alarm
There are a few detectable error and warning conditions with the sensors we have now:
- Unable to Obtain Pressure (UOP) Error – an attempt was made
- Unable to Maintain Pressure (UMP) Error – achieved pressure, but ran out of time holding it
- Unexpected State (UES) Error – a state transition that shouldn’t happen has occurred
- This one indicates a firmware bug or an unforeseen edge condition
- Position Over-extended (POE) Error – the pressure attempt failed by running out of room to squeeze
- POE always accompanies another error, depending on where in the state machine it happened
- Position Under-extended (PUE) Error – the machine never left the switch
- PUE is likely a mechanical failure that cannot be overcome without interference
- Incomplete Release (IR) Warning – not an error, but may lead to a POE eventually if stability isn’t achieved
- Over Pressure Detected (OPD) Warning – a pressure above the set maximum limit was detected
- Some additional logic should be applied in the host to determine when this becomes an error
PID Control Loop
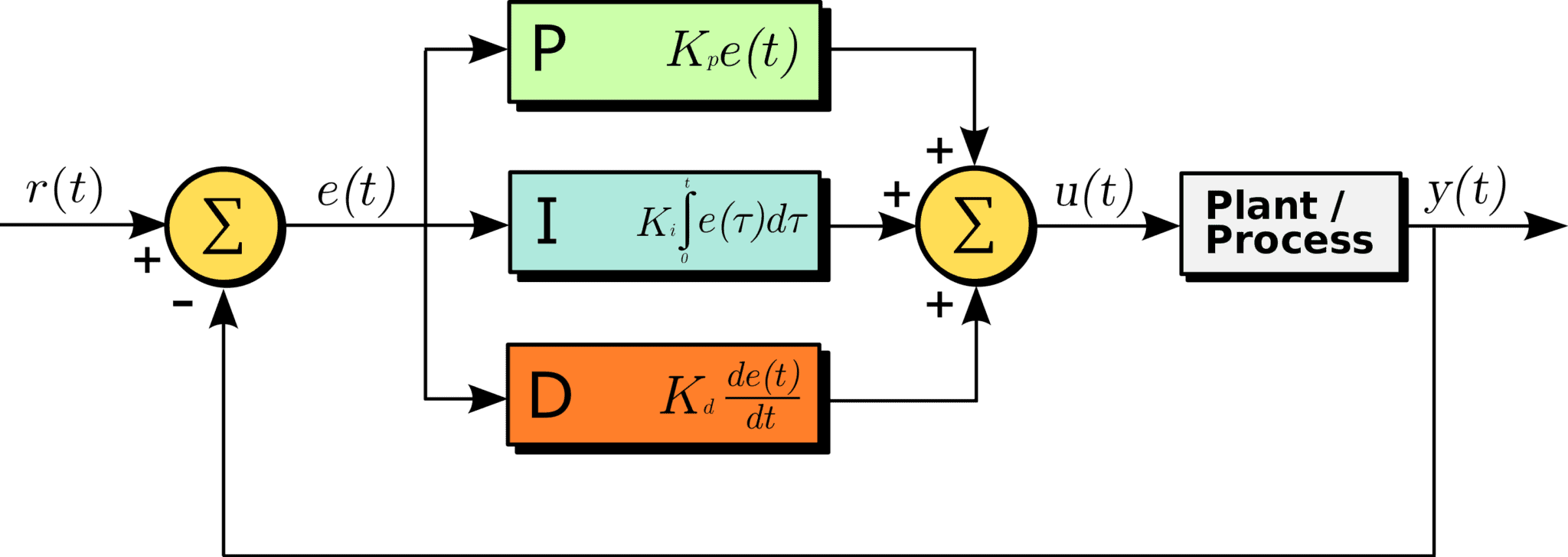
PID, short for Position-Integral-Derivative, is a method commonly employed to control small devices such as drone motors all the way up to process control of temperatures or pressures in factory machinery. It’s a large and complex topic, and a great place to start is the Wikipedia page.

To borrow a phrase from this great live document by Dr Erich Schulz, where he essentially describes how we utilize PID:
To illustrate the proportional response principle, ventilators should exhibit the agility of a balancing robot toy that is programmed to gently roll backward and forward until bumped to reverse direction. In our case, rather than rolling backwards and forwards, the ventilator is breathing in and out, changing airflow direction to closely track and assist the patient’s intrinsic respiratory efforts.
How the PID Control Loop Is Used
So the super-short explanation of PID: If given a targetinput, and an actual measurement such as the value from one or more sensors, at a semi-fixed interval (say, every millisecond) compute the error E as the difference of the measurement and the target, the integral I as this new error plus the previous integral value, and the derivative D as the difference of the previous error and this one. Then applying the user tunable parameters Pₓ, Iₓ, and Dₓ with the following formula you get a new output value O: O = Pₓ E + Iₓ I – Dₓ D. Loop ad infinitum.
When PID is used in a CNC machine, it’s typically used to control relatively expensive servo motors, which are basically a positional feedback sensor such as an encoder built into a powerful brushless motor. The encoder and PID loop makes these closed-loop motors. Closed-loop motors and their control electronics typically make servos much more expensive than simple open-loop (no feedback) stepper motors.
The other type of motor that’s typically used in CNC machinery is called a stepper motor. Stepper motors are designed in a such a way that they can electro-mechanically hold position in a set number of precise positions, with a 200-position motor being fairly typical. These motors are very popular (not just in CNC machinery) because they are inexpensive, easy to control, predictable without positional feedback, and readily available world-wide.
So here we’re doing something unusual, because we’re driving a stepper-motor with a PID loop indirectly, because our target is not a position, but instead is a set combination of pressure and volume. Since the link between the position and the target pressure/volume is non-linear and somewhat unpredictable due to part of the “mechanism” being a reactive and live human, we use a PID loop to control the velocity of the motor however it’s needed to achieve the target pressure/volume.
Electro-mechanically, this simplifies the control system by removing the need for positional feedback and reduces the cost accordingly.
About the Motion Control
One central theme of the g2core motion control system is that the motion is jerk-controlled. As velocity is the rate of change (derivative) of position, and acceleration is the rate of change of velocity, jerk is the rate of change of acceleration. BTW, the next derivatives are snap, crackle, and pop, really! Jerk is what roller-coaster engineers manage to ensure that you stay safely in your seat and don’t get whiplash.
g2core normally controls motion with constant-pop, as we plan motion coming in from Gcode files. It looks like this:
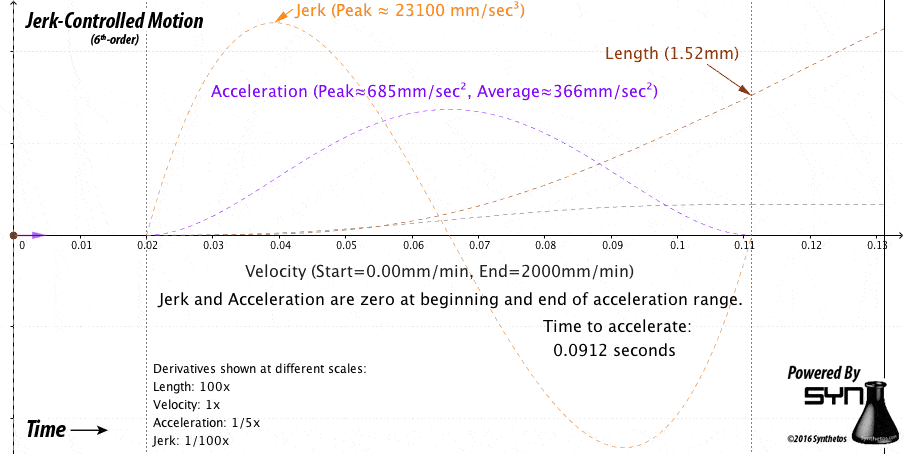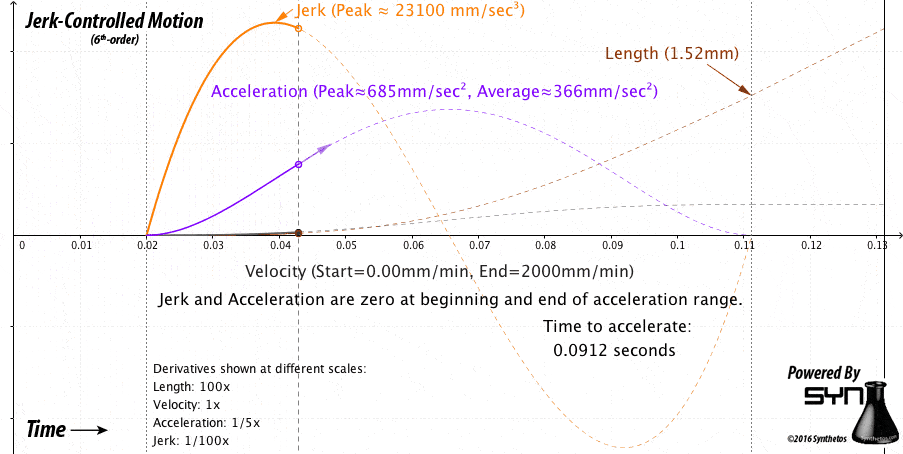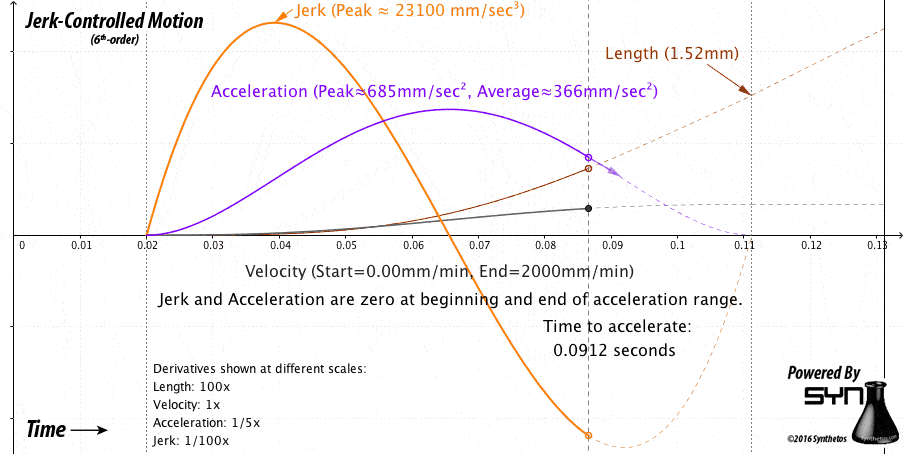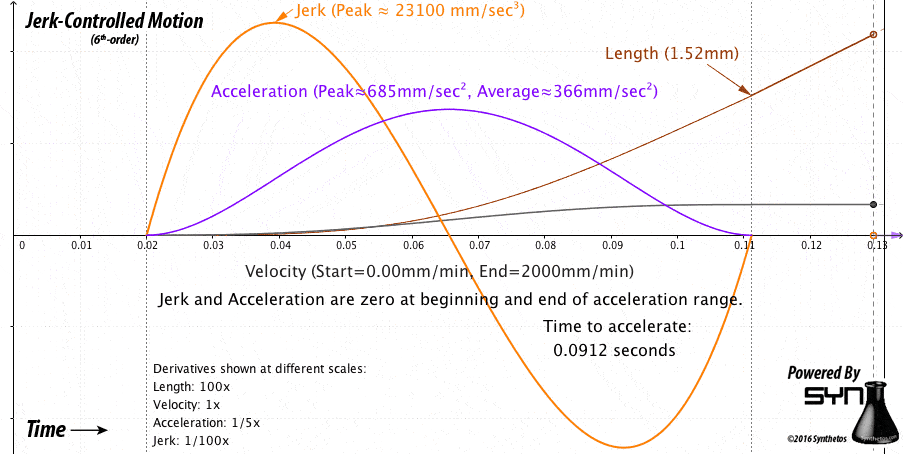
However, unplanned motion without set target positions and speeds is a slightly different problem, as we don’t know how long (in time or distance) that we have to get to a certain speed or to come to a stop. However, ten years of experience has taught us that jerk-bound acceleration will yield the most power from the motors, lowering the cost and raising the availability of parts.
Mathematically, this is non-trivial. The problem statement: given the output from the PID as a requested velocity, and the system knows the current velocity, current acceleration, and has been given a maximum jerk value. Assuming we simplify to a constant jerk implementation we would see something like the below in ideal conditions:
Note that we already have the mechanism to output motion in set time segments (nominally 1ms each) from the g2core kinematics system, and they are represented by a known current position, target position, start velocity, and end velocity. So, our goal is to determine what to set each of those value to per 1ms segment, and the system handles the rest. We also know the pressure reading and target pressure, both fed into the PID and with the output used as a target velocity. We also know the current position, velocity, and acceleration values. We need to ensure that the values we give it won’t violate max jerk (positive or negative) or the maximum velocity settings. There is no set limit on acceleration in g2core. We assume that we already limit the target velocity to stay within the system limits.
The naïve implementation is to compute the acceleration needed to achieve the velocity – which will likely be way more than we could achieve in 1ms – limit it to only changing by maximum positive or negative jerk, and then compute the new velocity and the resulting position. However, with an unbound acceleration, when we get to the target velocity we have a rather large non-zero acceleration, so we shoot right past it as we try to “wind-down” the oversized acceleration, resulting in wild oscillations. Further, if you “clip” the acceleration and drop it to zero then there is an instantaneous spike in jerk which causes a positional skip and the motor loses torque briefly. In this case, that means that the machine will stop generating pressure and the motor stops until the system realigns the velocity with reality.
The solution turns out to be relatively straightforward, but somewhat computationally intense. This is not a problem for our gQuintics running on an Arm Cortex-M7 with a floating-point co-processor, but would be somewhat impractical on an 8-bit system like the Arduino Uno.
The math is as follows, based on the well know constant-jerk formulas you can find explained nicely here:
Our goal is to achieve the target velocity with a final acceleration value of zero. So, if we arrange the acceleration formula to solve for t and set the target velocity (a_1) to 0, we get t= -a_0/j. If we replace t in the velocity formula, then solve for a_0, we get:
Now we have a function to use to determine our live acceleration limit in order to achieve target velocity with zero acceleration left over. Interestingly enough, you can see this function plotted in orange in the graph below, and that it’s non linear. To simplify the mechanism, and since precision in velocity is not necessary, we maintain a constant positive or negative maximum jerk, and constantly adjust the acceleration to get as close to the limit without violating it. In order to not end up on the wrong side of the limit, we look at least one segment ahead.
Next Steps
There’s still work to be done, and the project needs to adapt to the rapidly evolving COVID-19 situation and as we learn how best to treat it.
Please check out the project repo on GitHub, build a test unit, help us out. If you want to work with us more on this or you have a project of your own then let us know.
